Because the nature of this problem is to predict time series, methods specifically designed for this task should be tested. The well-known ones include:
And it is not hard to find out that customer flow is a seasonal time series. Therefore, time series decomposition such as X12 and STL may be useful tools in analysis.
Preprocessing
The datasets include plenty of information such as the user_id make a payment to shop_id at time. Because the goal is to predict the flow of each shop and it is hard to build a user_id profile based model with only this amount of data provided, a shop_id profile based solution appears to be a better choice, i.e., we will build a model for each shop, and do the prediction. Therefore, for the preprocessing, the user_id should be aggregated. This is a pretty entry level task for dpylr(R) or pandas(Python) user. Therefore, I do not share code for this part, the results are organized as following dataset:
library(psych)
summary(tc2017)
## shop_id time_stamp date_week nb_pay
## Min. : 1 Min. :2015-06-26 Monday :86544 Min. : 1.0
## 1st Qu.: 504 1st Qu.:2016-02-03 Tuesday :84851 1st Qu.: 51.0
## Median :1019 Median :2016-05-22 Wednesday:85283 Median : 82.0
## Mean :1008 Mean :2016-05-04 Thursday :85643 Mean : 116.3
## 3rd Qu.:1512 3rd Qu.:2016-08-15 Friday :86041 3rd Qu.: 135.0
## Max. :2000 Max. :2016-10-31 Saturday :84902 Max. :4704.0
## Sunday :86011
describe(tc2017)
## vars n mean sd median trimmed mad min max
## shop_id 1 599275 1007.58 577.88 1019 1008.69 747.23 1 2000
## time_stamp* 2 599275 NaN NA NA NaN NA Inf -Inf
## date_week* 3 599275 4.00 2.00 4 4.00 2.97 1 7
## nb_pay 4 599275 116.26 132.04 82 93.64 54.86 1 4704
## range skew kurtosis se
## shop_id 1999 -0.02 -1.22 0.75
## time_stamp* -Inf NA NA NA
## date_week* 6 0.00 -1.25 0.00
## nb_pay 4703 7.06 105.67 0.17
Exploratory
First, let us make some figures using off course ggplot2. Plots for first five shops:
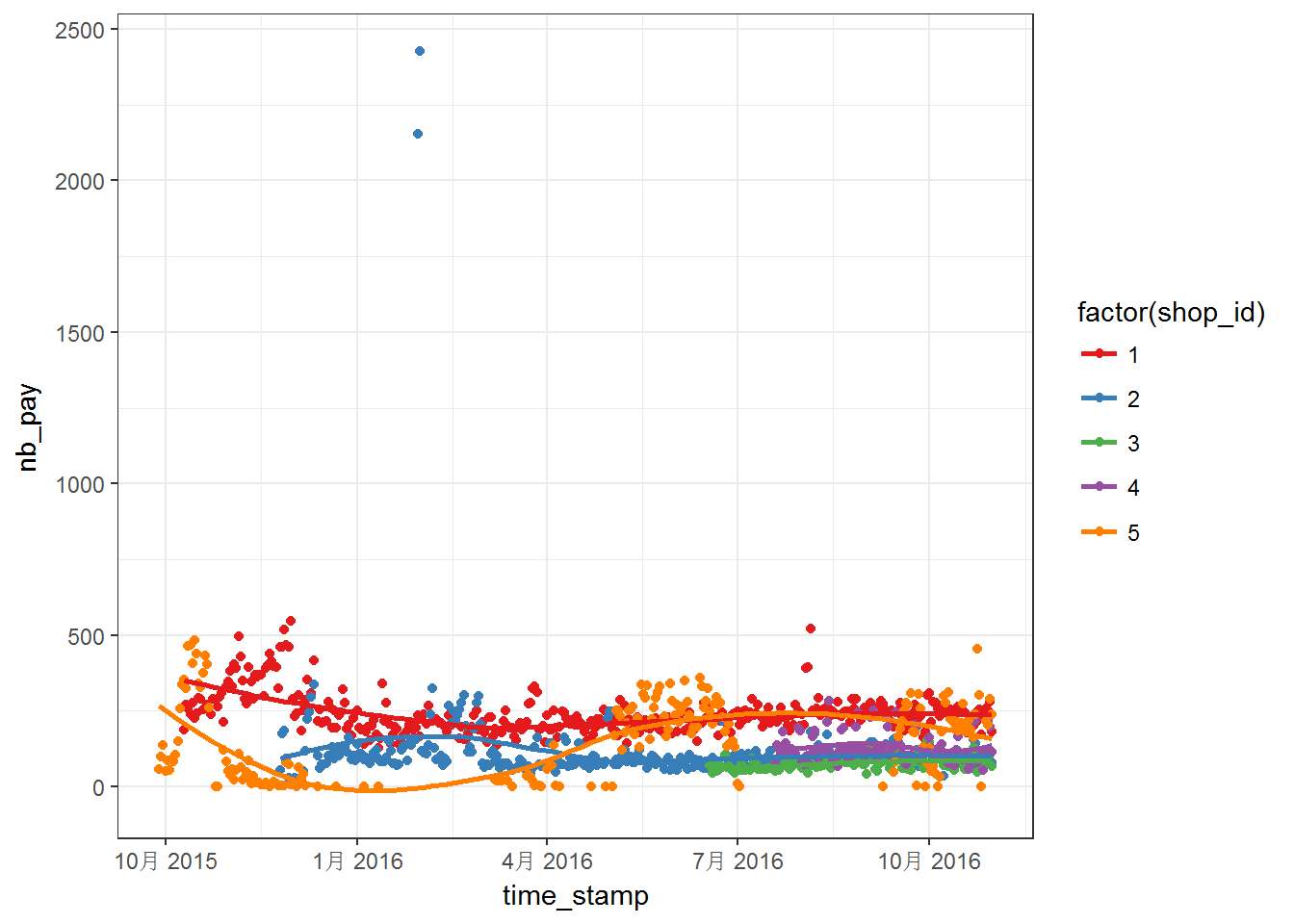
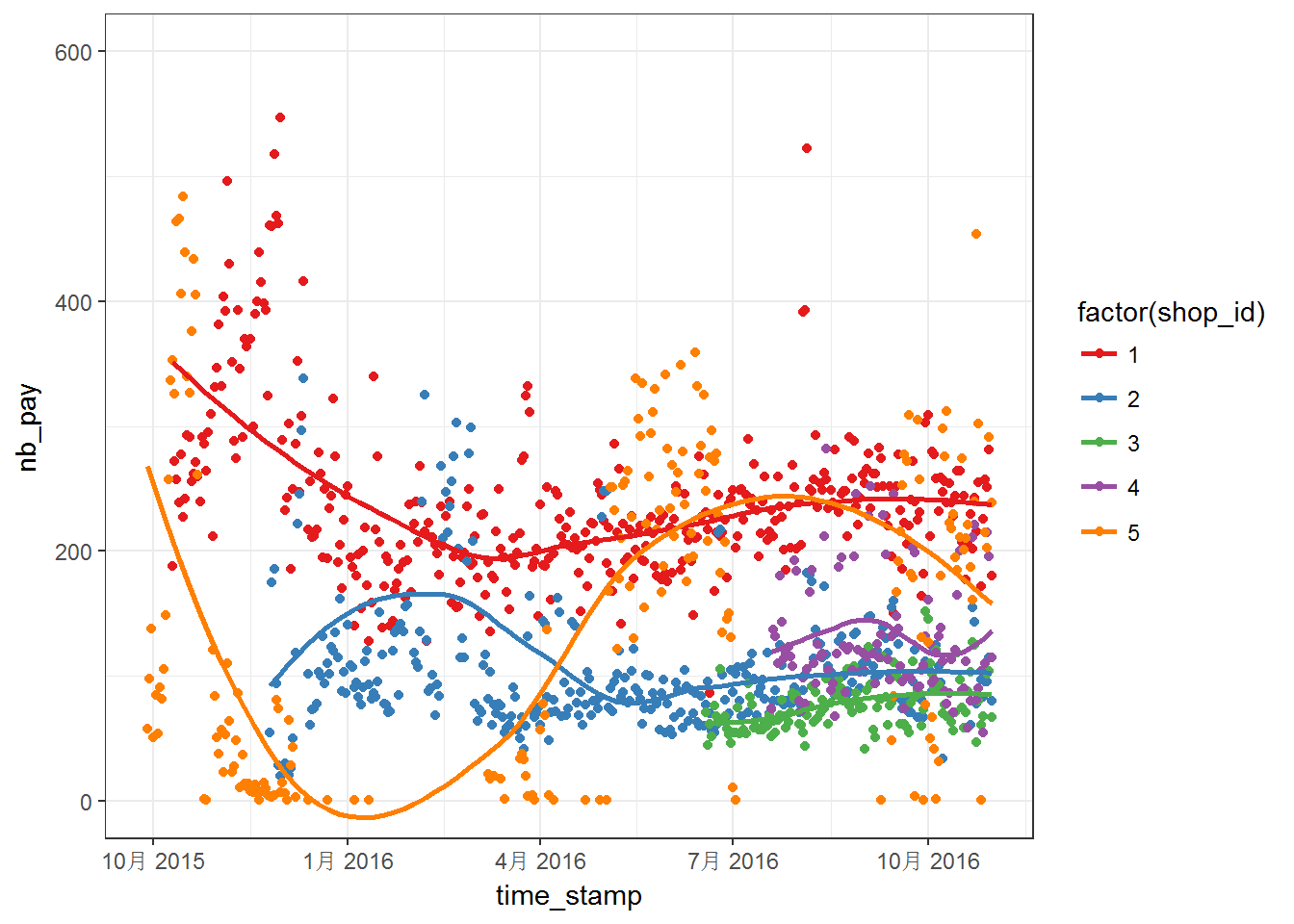
Above two figures are quite messy. We can notice that the data have different range, which means that we may have to worry about NAs. Moreover, most of the series do not steady in the given range. For these five curves, the curves are more steady after April 2016. Then, above series are plotted into separated panels as follows:
p <- ggplot(tc2017 %>% filter(shop_id<6),aes(time_stamp,nb_pay)) +
geom_line() +
facet_wrap(~shop_id, ncol = 1, scales = "free")
print(p)
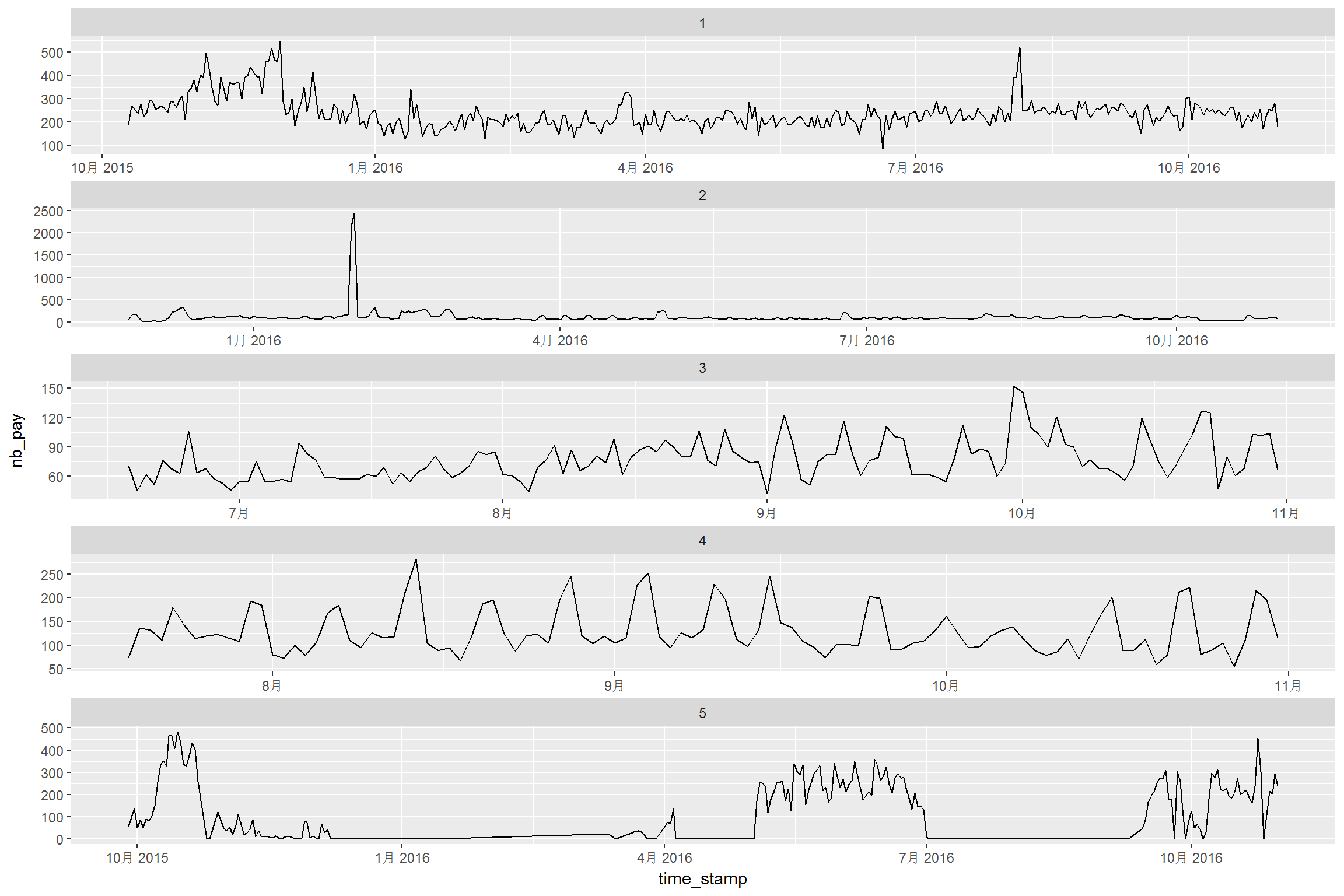
Some series have strong seasonal feature, such as curve for shop_id==4. We may need to consider the seasonal effect. A quick acf drawing is shown as below:
acf((tc2017 %>% filter(shop_id==4))$nb_pay)
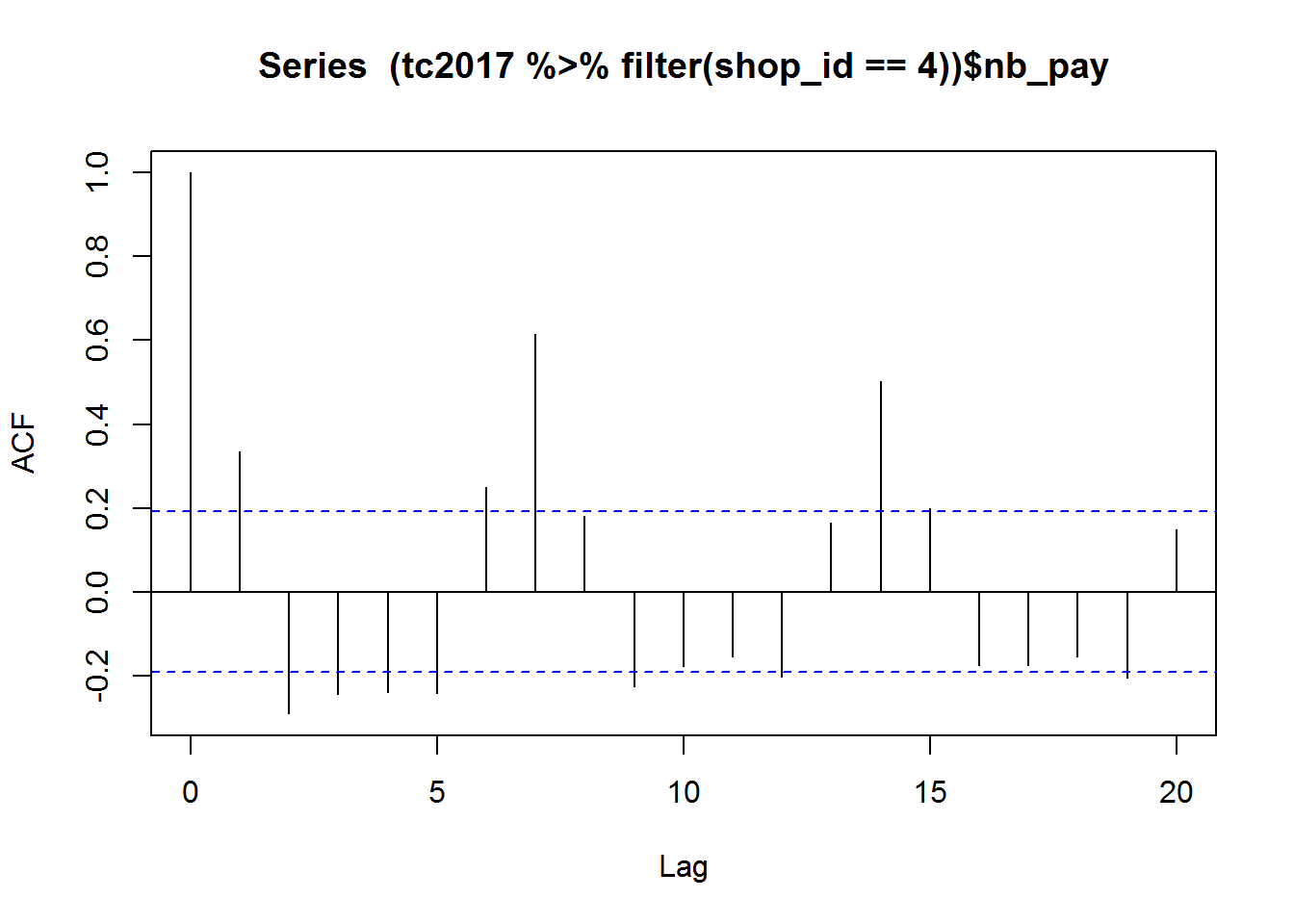
It can be observed that the periodic pattern is quite clear, the period is 7 and it is the length of one week. Therefore, we plot the data against the weekday:
p <- ggplot(tc2017 %>% filter(shop_id==4),
aes(time_stamp,nb_pay)) +
geom_line(size=1) +
facet_grid(date_week~.,scales = "fixed")+
theme_bw()
print(p)
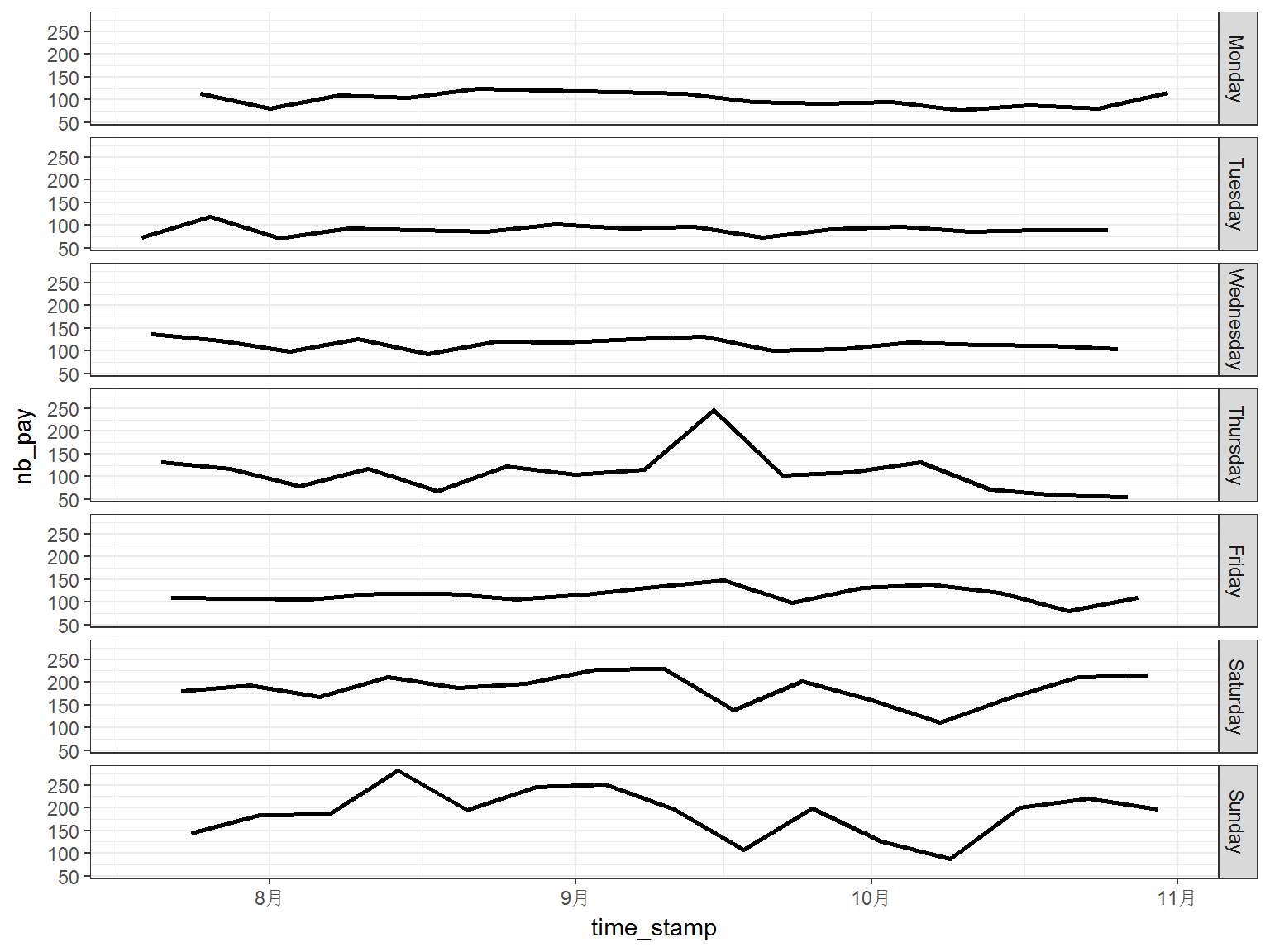
It is shown in above figure, the number of customs is much steady when we investigate the flow on the same weekday. This pattern also appears in the data of other shops.
p <- ggplot(tc2017 %>% filter(shop_id<6),
aes(time_stamp,nb_pay,color = date_week)) +
geom_line(size=1) +
facet_grid(date_week~shop_id,scales = "free")+
scale_color_brewer(palette = "Set1")+
theme_bw()+ theme(legend.position = "none")
print(p)
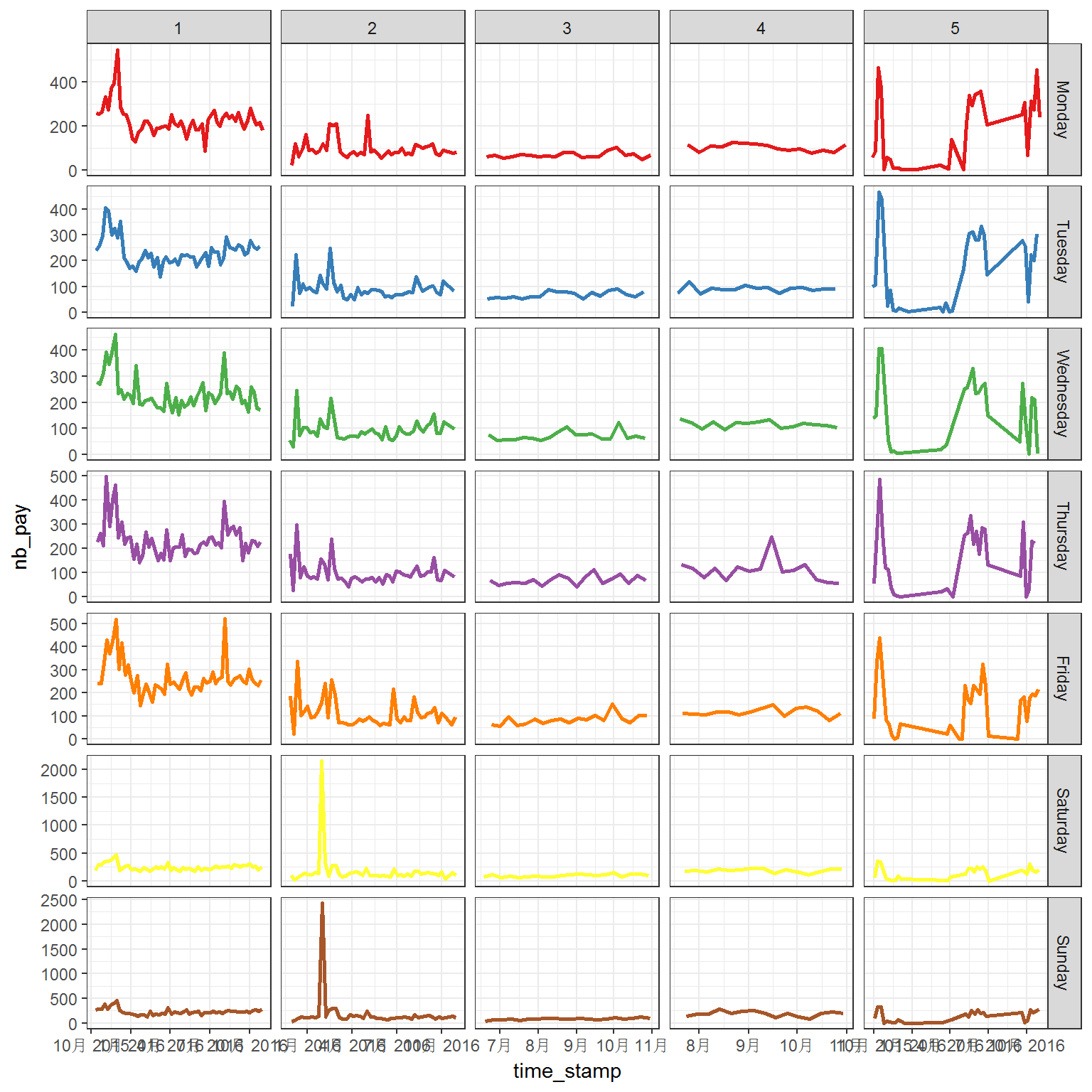
Generally, the flows have quite different patterns between weekdays and weekends. However, the longtime trend also plays important role in the flow.
Let's make some predictions here:
library(forecast)
library(xts)
to.ts <- function (x) {
ts(x$nb_pay,frequency = 7)
}






